논문 링크 Efficiently Modeling Long Sequences with Structured State Spaces
특징 : ICRL 2022 Outstanding Paper, 인용 수 1578회 (2025-01-25 기준)
코드: https://github.com/state-spaces/s4
GitHub - state-spaces/s4: Structured state space sequence models
Structured state space sequence models. Contribute to state-spaces/s4 development by creating an account on GitHub.
github.com
1. Preliminaries
해당 논문을 이해하기 위해 저자인 Albert Gu가 작성한 두 편의 논문을 참고할 필요가 있다.
- HiPPO: Recurrent Memory with Optimal Polynomial Projections
- Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
1.1. HiPPO: Recurrent Memory with Optimal Polynomial Projections
첫 번째 논문인 HiPPO의 경우 RNN 계열(LSTM, GRU 등)의 모델은 고정된 차원의 hidden state를 넘겨주면서 과거의 정보를 전달하는데 이때 "어떻게 하면 과거의 정보를 잘 압축해서 전달할 수 있을까?"에 대해 HiPPO Framework를 제안한다.
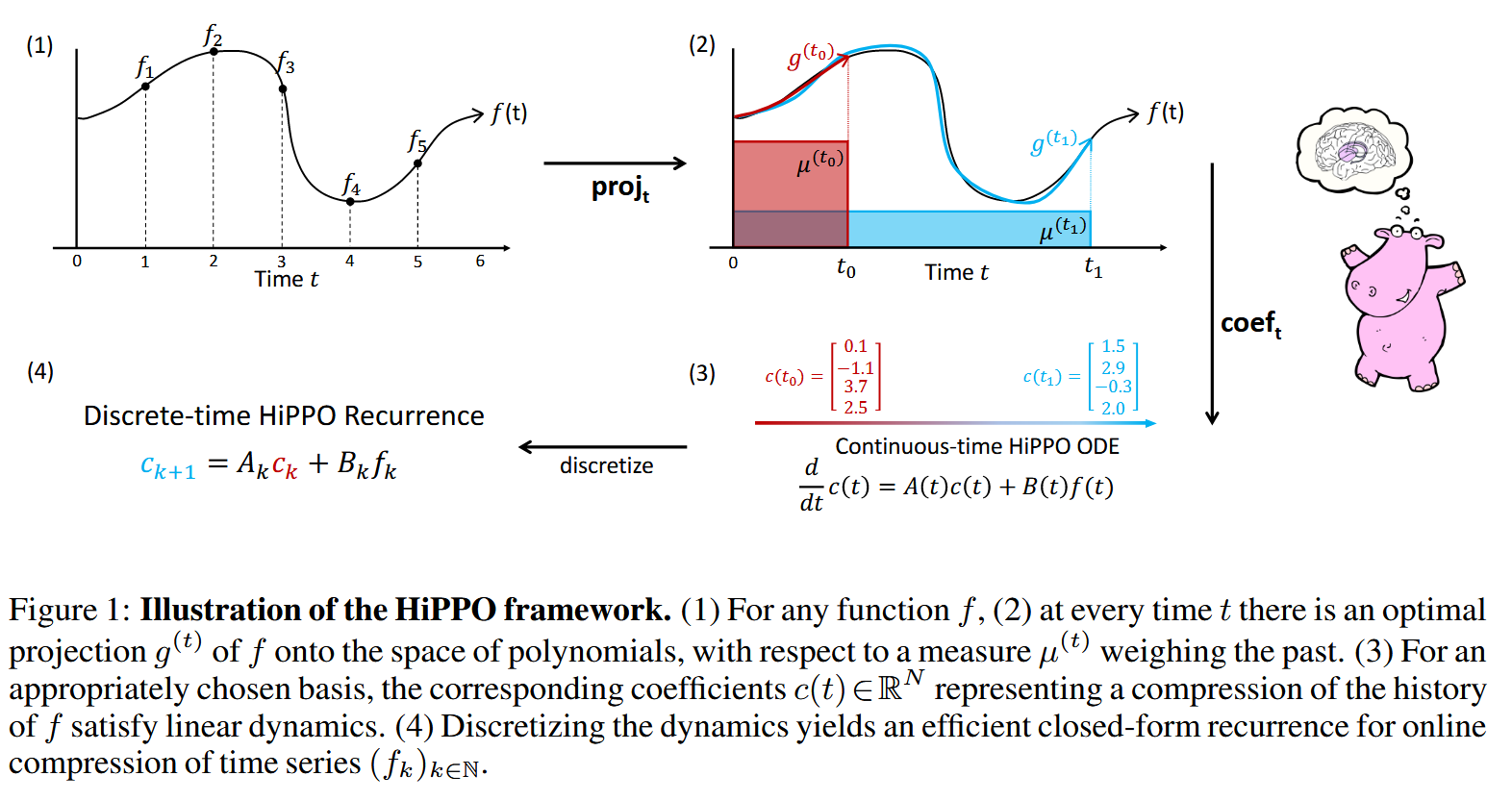
HiPPO는 hidden state가 시간이 지남에 따라 이동하는 모습을 근사하는 것이다. 구체적으로는 어떠한 입력을 받아서 hidden state를 출력하는 함수를 f라고 할 때 (이 함수의 공간이 넓기 때문에) f를 subspace G에 projection하고 이를 1~N차원의 Legendre orthogonal basis의 coefficient로 표현한다.
(왜 Legendre인가? - 논문 Appendix에서 저자는 Neurobio분야 논문에서 다음과 같은 결과가 나왔기 때문이라고 설명: “선형 시간 불변(LTI) 동적 시스템을 Pade approximants로 동적 근사했을 때 그 결과가 우연히 Legendre polynomials의 형태로 도출된다”)



이때 이 continuous한 근사 과정을 discretization하게 되면 첫 번째 이미지 왼쪽아래 수식처럼 A와 B의 파라미터를 가진 수식으로 표현되는데 이때 A는 학습되는 파라미터가 아니라 수치적 기법을 통해 구해진 HiPPO matrix A로 고정되며 실제로 random initialize한 모델보다 좋은 결과를 보였다.
1.2. Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
두 번째 논문인 LSSL(Linear State Space Layer)의 경우 기존 HiPPO과의 몇 가지 차이점을 보이는데 이는 다음과 같다.
(1) HiPPO matrix A는 polynomial basis의 내적 계산 시 사용되는 measure (=어떤 시간에 가중치를 둘 것인지)를 LegS (=theta 기간 동안 동일 가중 평균)로 설정했을 때 적용되는 특화된 행렬인 반면 LSSL에서는 그 외 다른 measure에 대해서도 gerneralized된 행렬 A를 수학적 증명으로 보이며 고정된 A행렬이 아닌 학습가능한 A 행렬이되 초기 값을 HiPPO 행렬로 둔다.
(2) HiPPO는 RNN에 부착된 operator로서 작동하기 때문에 병렬 연산이 작동하지 않고 vanishing gradient 문제가 발생하지만 LSSL에서는 하나의 layer로서 적용되고 비선형 함수가 Layer 내에 존재하지 않기 때문에 convolution처럼 병렬 연산을 진행할 수 있다.
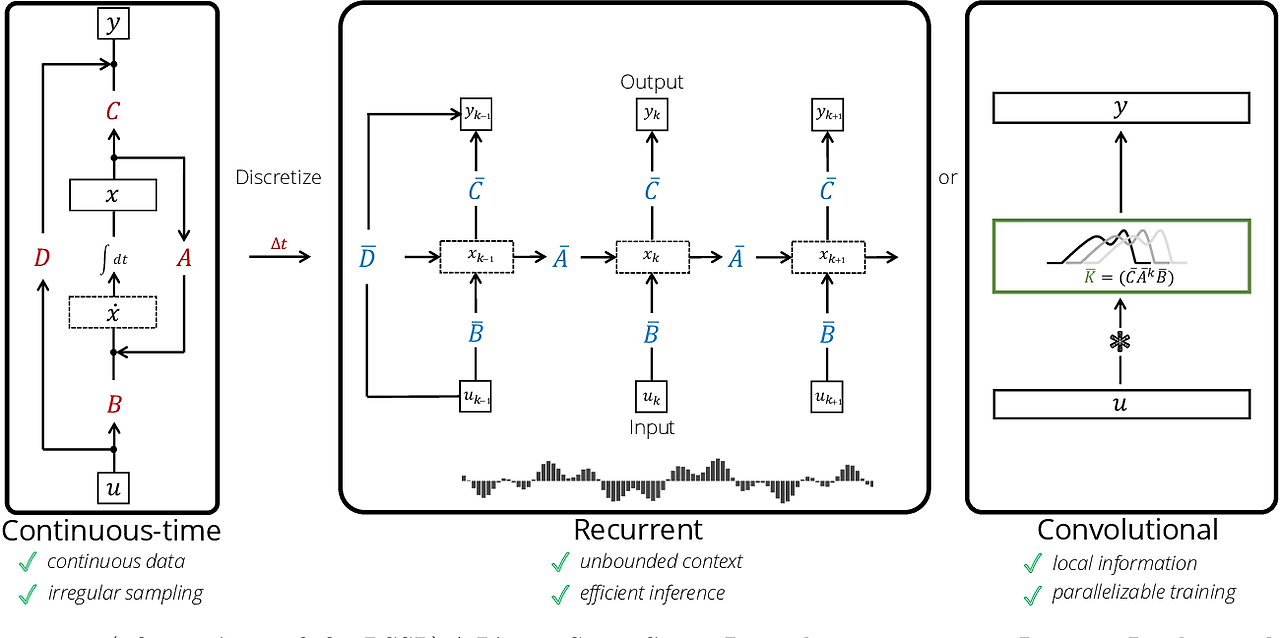
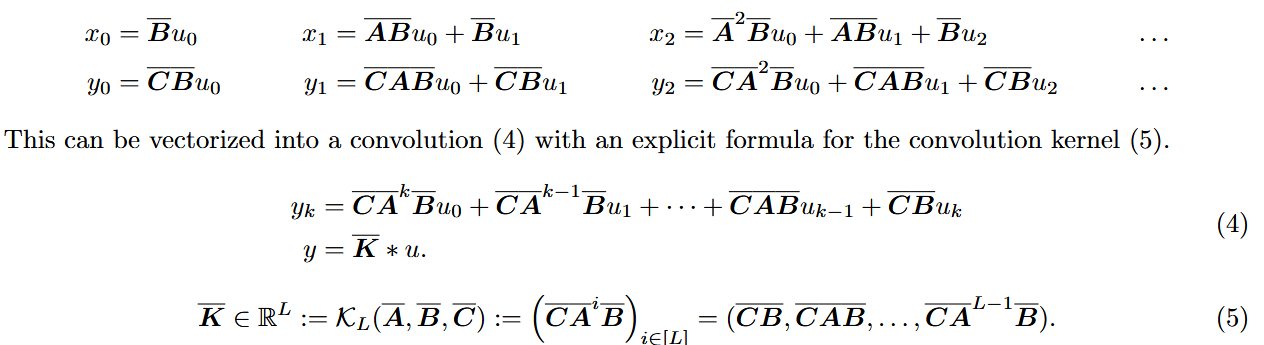

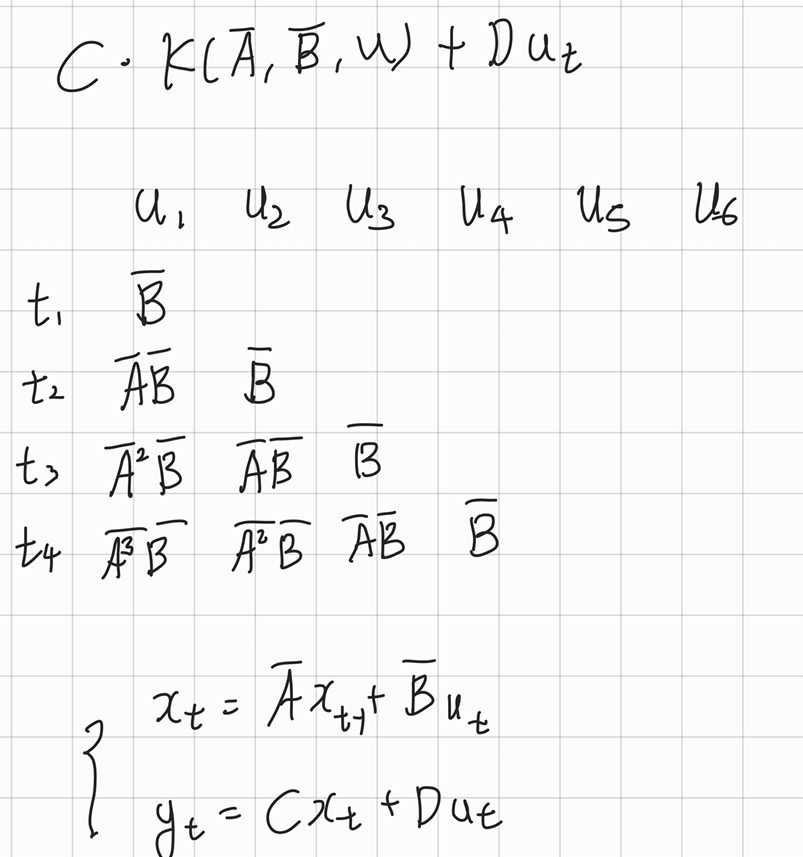
즉 간단히 말해 B, AB, A^2B, ..., A^kB를 계산하여 준비하고 벡터 u에 대해 convolution의 형식으로 연산을 진행한다.
2. Methodology
"Efficiently Modeling Long Sequences with Structured State Spaces" 논문에서는 기존 LSSL이 연산 시 행렬 A를 반복적으로 곱하는 과정을 효율적으로 처리하고자 했다. 그 과정에서 선형대수의 Diagonalization이라는 개념을 활용했으며 이를 통해 Diagonal 행렬 Λ 의 대각 element만 제곱해주는 방식으로 계산량을 줄였고 이를 Structured State Space Sequence model(S4)라고 부른다.
(참고 - Diagonalization 행렬은 제곱하게 되면 X와 X inverse가 만나면서 제거되고 중간에 있는 Diagonal matrix만 제곱되는 형태가 됨)

조금 더 구체적으로는 Normal Plus Low-Rank(NPLR) 방식을 사용했는데 간단하게 설명하자면 A행렬이 Normal하지 않기 때문에 diagonalizable하지 않고 그렇기 때문에 PQ^T를 사용하여 diagonalizable한 부분 (=Normal한 부분)과 Low-rank인 부분으로 나눴다. (이때 A의 초기 값은 LSSL과 마찬가지로 HiPPO matrix로 초기화했다.)
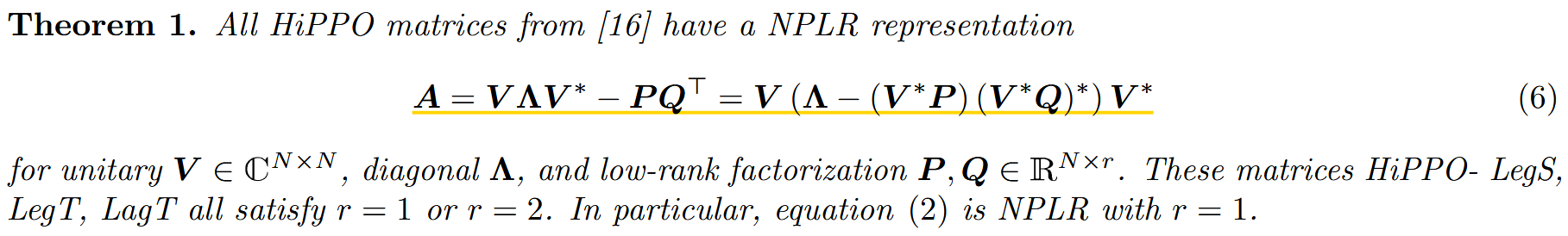
3. Results
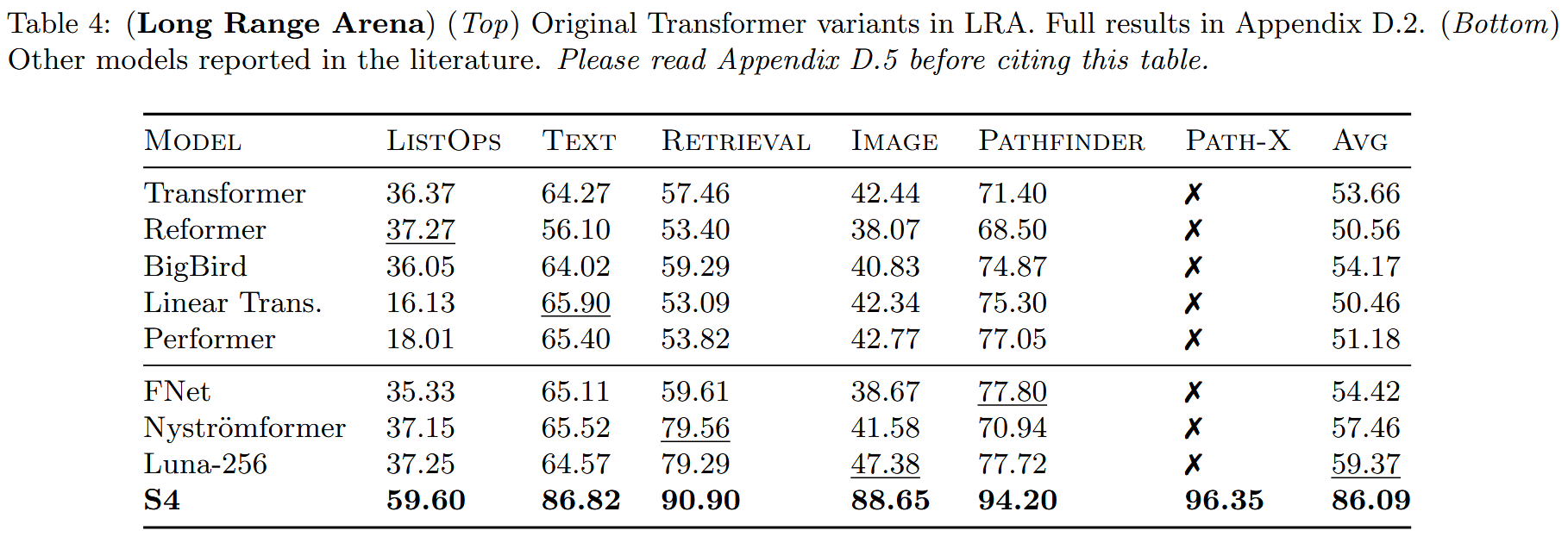
이러한 모델들은 Linear RNN 혹은 State-Space Model이라고 하는데 이 종류의 모델들은 "Long Range Arena"라고 하는 장기 의존성 문제에서 상당히 높은 성능을 보였다. 심지어 transformer보다 압도적인 성능차이를 보였다.
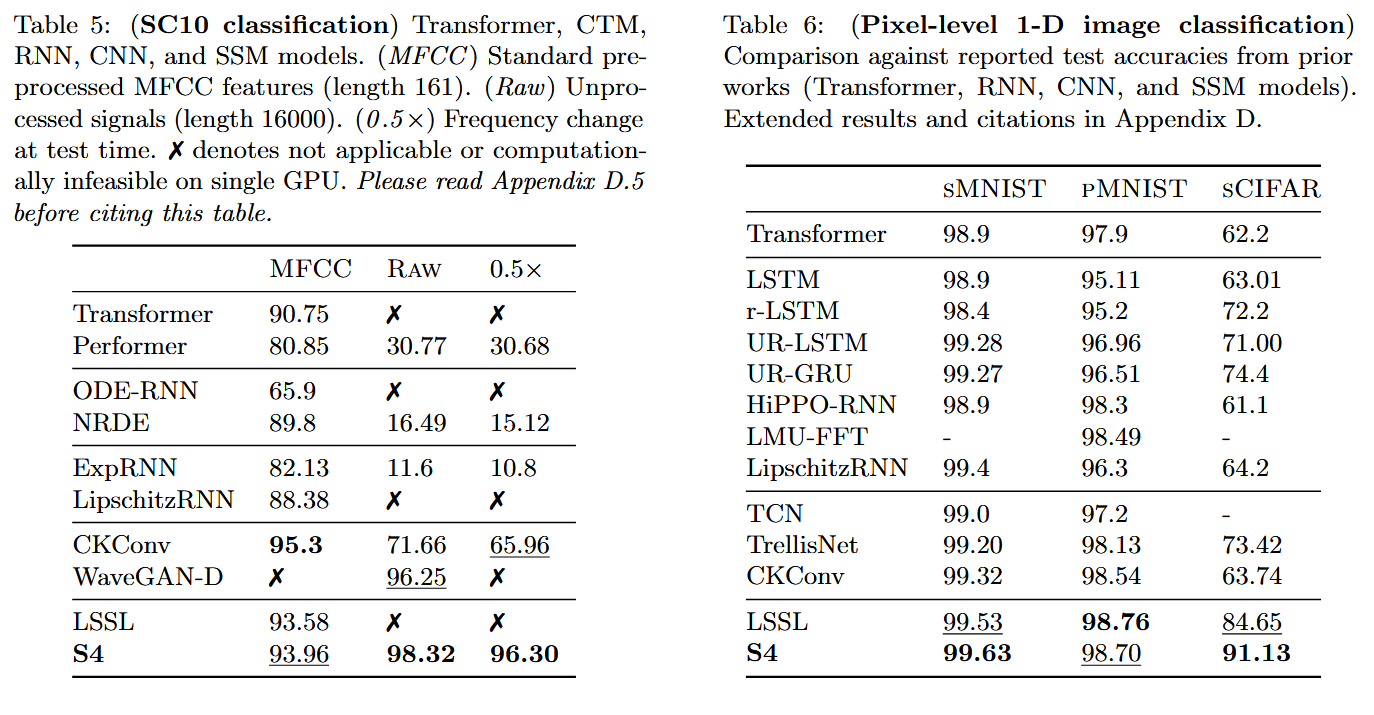
이외에도 오디오, 이미지 모달리티에서도 높은 성능을 보였는데 특히 오디오의 경우 일반적인 전처리 방법인 MFCC를 적용하지 않은 Raw data에서 높은 성능을 보였다.
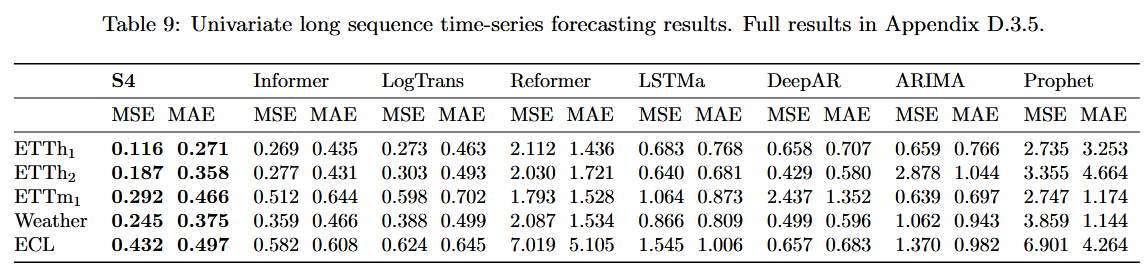
단변수 시계열 예측에서도 기존 시계열 예측 SOTA 모델인 Informer의 성능을 뛰어넘었다.
4. Ablation
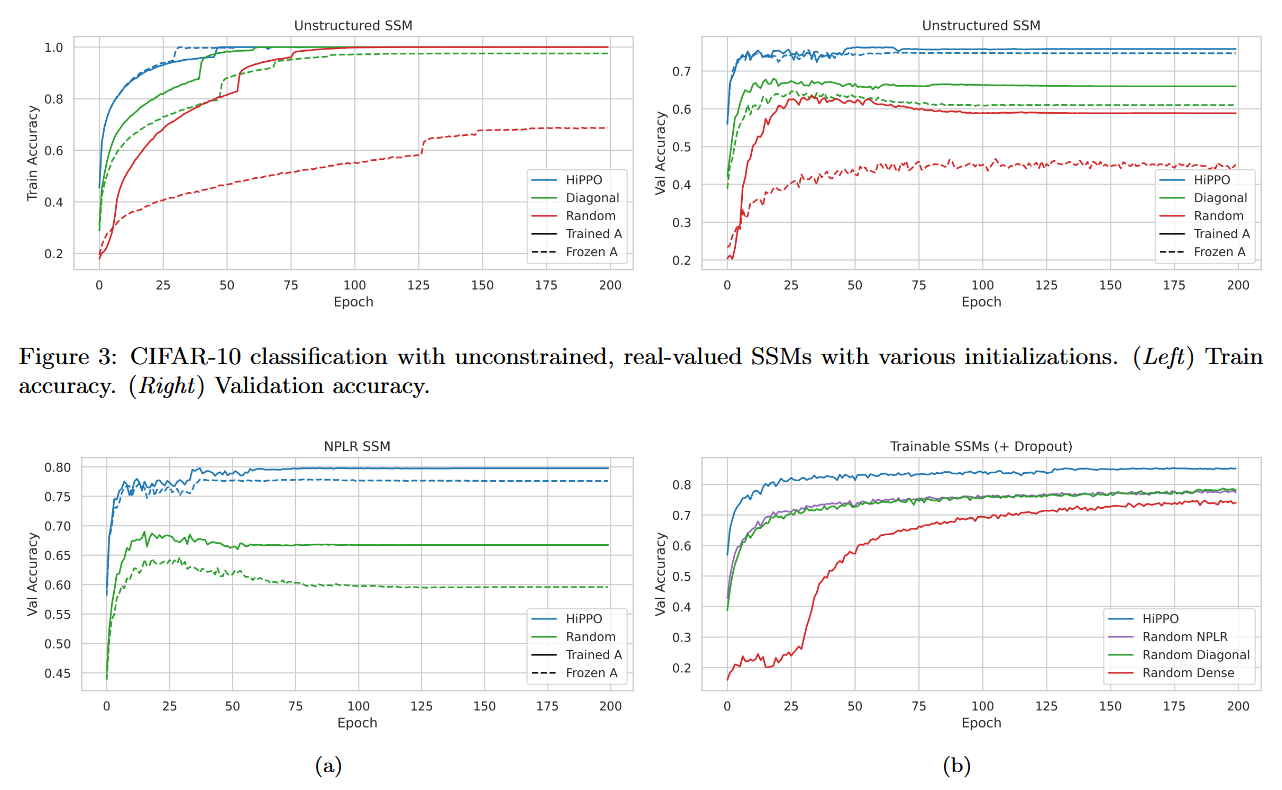
모델의 성능은 NPLR보다는 HiPPO matrix로 초기화했다는 점이 주요한 요인인데 이는 아래 그래프에서 확인할 수 있다.
Figure 3 왼쪽(Train Acc)와 오른쪽(Validation Acc)을 보면 Validation에서 큰 gap을 보이며 높은 성능을 자랑한다.
5. Personal Review
(1) 대부분의 데이터 셋 결과가 1-D dimension(즉 1차원 입력과 1차원 출력)에서 좋은 결과가 나왔기 때문에 multi-dimension에서의 결과를 업데이트할 필요가 있다.
(2) 이 모델은 sequence가 긴 long-range dependency와 관련된 task에서 높은 성능을 보인다.
(3) 또한 continuous-time에 대해 근사하는 방법을 사용했기 때문에 데이터의 irregularity에도 robust한 강점을 보인다.
